„The goal of maths and design education is to develop a way of thinking.“ John Clark Kiehl & Ruth Mateus-Berr The fascination for maths, art and design was initiated by the project „design-goes-maths“. This was a collaboration between the Viennese University of Applied Arts, Technical University and University of Vienna/ Educational-Sciences. Under the leadership of Dr.Ruth Mateus-Berr some students, artists, designers and mathematicinas, Walter Lunzer meanwhile, kept on working on this topic and founded the „Applied Design-Thinking-Lab/ Vienna“. The lab combines scientific topics with art and design. Main purpose is to develop new approaches for sciences as well as to improve distribution of scientific knowledge by using methods of visualisation, performance, and art-education.

Platonic Solids:Through Dimacs-Conference we got an invitation from the international Bridges Conference. This is an annual meeting of artists, designers and mathematicians from all over the world, which we started to participate several times. During this period a artificial research on Platonic solids started

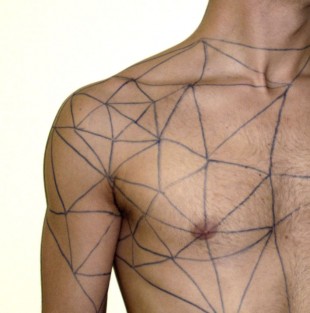
Platonic solids are built from regular polygons: equilateral triangles (icosahedra and tetrahedra), pentagons (dodecahedra) or squares (cubes). Dodecahedra and icosahedra are convex shapes, like all platonic solids, but these two in particular are quite close to the sphere. Consequently these two are interesting to use on the body: Body parts like the shoulders, head, derriere or breasts, and fashion pieces like puffed sleeves, crinolines, and hats resemble hemispheres, and therefore could be modelled using icosahedra or dodecahedra.

Dodekahedron-Blouson white tull, pattern made out of pentagons: The challenge embodies multiplying one single flat shape (like a pentagon or an equilateral triangle), putting them together in order to design a garment. The advantage is that each line fits with every other, so it is not necessary to measure the time. Additionally we gained form and seams we could hardly get by usual patternmaking, thus making this approach conceivably have the greatest creative impact. Using icosahedra to start with, we quickly came close to the technique called triangulation, which is often used for animating figures in film.

This series of artworks is based on a computer-program called „polynomiography“ which visualizes polynom-functions. It was invented by Prof. Bahman Kalantari/ Rutgers University New Jersey. He invited the Applied Design-Thinking-Lab/Vienna to work with his program artificially and to present our works at DIMACS-Conference (Centre for Discrete Mathematics and Theoretical Computer Science, New-Jersey).

Soft-pets inspired by a polynomiography: silk, glas-beads, feathers. 25x17x10cm

paintings inspired by a polynomiography water-colour on paper, 20x30cm

paintings inspired by a polynomiography water-colour on paper, 20x30cm

Soft-pets inspired by a polynomiography: lycra, 21x16x12cm

Soft-pets inspired by a polynomiography: lycra, 35x10x3cm

Mathematical Business-cards communication tool: The image of maths, as a highly complex, difficult or absurd field of studies needs be improved. Those who are not into maths mostly confuse maths with calculating. But higher maths is far more! It is worth thinking and discussing mathematical topics, even if you are not studying it. You quickly cross topics of philosophy, realism, dimensions, and fiction. flexi-foils on Paper, 8x5cm, flex cards back and forth to make image move

Mathematical Business-cards communication tool: To trigger mathematical conversation in daily life mathematical businesscards has been developed which introduce topics of higher maths. Two examples have been produced. One is coping with the phenomenon of Hilbert’s Hotel; one is showing the paradox of Banach-Tarski. Team TU Wien: Birgit Hischenhuber, Sarah Rathbauer Angewandte: Mathias Kendler, Walter Lunzer, David Ölz flexi-foils on Paper, 8x5cm, flex cards back and forth to make image move